Rechenpower im Überfluss? – Intelligenz gegen pure Kraft

Ein Appell an die Berechnungsingenieure, wieder mehr Hirn einzusetzen
Immer wieder begegnen mir bei meinen Mitarbeitern aber auch bei unseren Kunden Rechenmodelle, die wahnsinnig kompliziert aufgebaut sind und leider so lange rechnen, dass damit zeitnah keine vernünftigen Optimierungen gemacht werden können. Die Endergebnisse sind unzufriedene Kunden, welche die notwendigen Ergebnisse für ihre Schlussfolgerungen zu spät erhalten.
Da ich zu meinen Anfangszeiten als Berechnungsingenieur Ende der 80er Jahre nur sehr beschränkte Ressourcen zur Verfügung hatte, war ich darauf angewiesen, die Aufgabenstellungen eher intelligent und nicht mit Kraft (Rechenpower) zu lösen.
Die Rechenpower hat sich in den 32 Jahren, in denen ich nun im Geschäft bin, alleine in meiner Firma um mehr als den Faktor 1.000.000 erhöht.
Nun ist aber
Leistung = Arbeit pro Zeitaufwand
Nutzt man nur die gestiegene Rechenpower und macht sich gleichzeitig immer weniger Gedanken, wie man die erforderliche Rechenzeit intelligent reduzieren kann, vergeudet man Ressourcen und die Leistung ist schlechter, als sie sein könnte.
Das ist vergleichbar mit einem Auto mit einem löchrigen Tank, bei dem immer leistungsfähigere Motoren einbaut werden, um Sprit zu sparen.
Grundlagen
Schauen wir uns die Grundlagen an.
Numerik, ob Strömungssimulation oder Struktursimulation, hat grundsätzlich etwas mit Diskretisieren zu tun.
Diskretisieren bedeutet, aus einer Vielzahl von möglichen Punkten (dem Kontinuum) endlich viele (diskrete) Punkte auszuwählen, an denen man Ergebnisse haben möchte.
Warum? Auch der leistungsfähigste Rechner hat mit der Unendlichkeit so seine Probleme.
Der allgemeinste Fall für eine Simulation bedeutet, dass sich die Ergebnisse mit der Zeit im Raum ändern.
Also muss man auch die Zeit diskretisieren, um das zeitliche Verhalten bestimmen zu können.
Ändert sich in der Realität ein Wert stark (räumlich oder zeitlich), muss die Dichte der diskreten Punkte größer sein als in Bereichen, bei denen die Ergebnisse nahezu konstant bleiben. Sonst kommt nichts Sinnvolles dabei raus.
Ein Beispiel dafür sind die Spannungen in einem Kerbradius. Ein Element über den Radius ist einfach zu wenig.
Auch sollten die Abstände zwischen den Punkten nicht schlagartig zu- oder abnehmen, da die Lösungsalgorithmen dann Schwierigkeiten bekommen.
Rechenzeit
Die benötigte Rechenzeit verhält sich in etwa quadratisch zur Anzahl der Punkte (Knoten, Elemente, Volumen, Partikel) und linear zu den Zeitschritten.
Daher sollte eine intelligente Modellerstellung / Vernetzung zuerst bei der Anzahl der Elemente ansetzen.
Die räumliche Diskretisierung
Die Anzahl der Elemente lassen sich durch die Verwendung von Symmetrieeigenschaften drastisch reduzieren. Allerdings sind an den Symmetrieebenen geeignete Randbedingungen zu wählen, was nicht immer ganz einfach ist und wo oft Fehler gemacht werden.
Dünne Strukturen lassen sich über Schalenelemente wesentlich genauer beschreiben und rechnen dabei schneller. Stabähnliche Strukturen können durch die Verwendung von Balken wesentlich effizienter berechnet werden.
Und da gibt es noch den ebenen Spannungszustand, den ebenen Dehnungszustand und den rotationssymmetrischen Zustand, den man auch noch heranziehen könnte. Die wenigsten kennen noch den Unterschied zwischen ebenem Spannungszustand und ebenem Dehnungszustand.
Vereinfachungen im Modell
Im Strömungsbereich lassen sich z.B. Lochbleche durch poröse Medien vereinfachen und aus einem Modell mit mehreren Millionen
Volumenelementen wird ein Modell mit 500.000 Elementen. Rechenzeiten können so schnell um den Faktor 10 – 100 schneller rechnen.
Ein weiterer Tipp: Wird die Dicke des porösen Mediums erhöht und die Porosität reduziert, verbessert sich das Konvergenzverhalten erheblich. Die Ergebnisse werden dadurch kaum beeinflusst.
Beispiel:
Die Bestimmung des Druckverlustes durch ein 1 m x 1 m Lochsieb lässt sich beschreiben durch
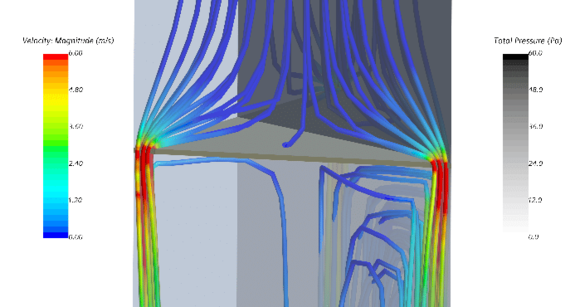
– Eine 3D-Simulation des Gesamtmodells (Abbildung 1)
– Eine 3D-Simulation eines Ausschnitts
– Eine 3D-Simulation eines symmetrischen Modells einer Bohrung mit entsprechenden Randbedingungen (Abbildung 2).
Das Ergebnis: Nahezu identisch, die Abweichung ist < 3%. Die Rechenzeiten sinken von 1 Stunde auf weniger als 1 Minute. Dies sind fast zwei Größenordnungen!
Kalibriert man nun ein poröses Medium, kann das Lochblech im Gesamtmodell dadurch ersetzt werden und globale Aussagen lassen sich im Bereich von Minuten treffen, anstatt Tage zu warten.
Die zeitliche Diskretisierung
Oft wird die Zeitschrittweite bei Berechnungen konstant gehalten, obwohl die Ergebnisse sich logarithmisch verhalten. Eine logarithmische Zeitschrittweite verkürzt die Rechenzeit und den Speicherbedarf dramatisch.
Logarithmisches Verhalten ist z.B. bei Kriechen, Temperaturentwicklungen oder Konzentrationsentwicklungen der Fall.
Versuchen Sie mal, statt konstanten Zeitschritten eine angepasste Zeitskala zu verwenden. Um ungerade Zeitpunkte zu vermeiden, habe ich hier folgende Zeitschritte verwendet:
1,2,5,10,20,50,100,200,500,1000,2000,5000,10000 ….
200.000 Stunden Kriechen (22 Jahre) lassen sich damit in nur 17 Zeitschritten beschreiben.
Natürlich freue ich mich, wenn sich die Rechenleistung alle 18 Monate verdoppelt, weil dann kann ich irgendwann noch zu Lebzeiten einen Zementtrockner mit einer Länge von 10 m mit Partikelgrößen von 0,1 mm rechnen (bzw. rechnen lassen 😊).
Ein Rechenmodell, das bei gleicher Aussagefähigkeit wesentlich weniger Rechenpower benötigt, ist immer intelligenter und letztendlich der schnellere und effizientere Weg!
Ihr Stefan Merkle

PS: Suchen Sie intelligente Lösungen? Dann sind Sie bei uns richtig!







Kommentare und Antworten
Bemerkungen :
Schöne Grüße aus dem Süden