Finite element method (FEM for short)

The finite element method (FEM or FEA for finite element analysis) is a numerical calculation method for calculating the strength and behaviour of bodies under the influence of physical force.
Like CFD flow simulation, it belongs to the virtual simulation methods, which are also generally summarised under the term CAE (Computer Aided Engineering).

In design practice, FEM simulation is used to examine the load-bearing capacity of components in advance without practical tests. By reducing or even replacing costly tests on prototypes, development costs and development times can be drastically reduced. Virtual simulations can also be used to calculate far more scenarios of the most varied load situations and boundary conditions than can be tested by trials. As a result, products can be optimised much more efficiently and precisely, not only in terms of strength, but also in terms of structure, construction and design. Material can also be saved at less stressed points, which ultimately has an effect not only on material costs but also on weight. There are special processes that are modelled on bionics, i.e. the adaptation of nature in the course of evolution. The classic example here is the horsetail, which optimally combines stiffness and flexibility without breaking in a storm.

Your advantages through FEM simulations: You know more about the behaviour of your components, can see what is otherwise invisible and thus gain additional safety.
In short, you save time, money and nerves in the development of your products and are one step ahead of your competition.
What is the underlying theory of a finite element calculation?
In the finite element method, the problem or the calculation area is divided into a finite number of elements.
The equations (usually differential equations) are then solved for each of these elements. The results then provide information about the entire calculation area. The number of elements determines the accuracy of the overall results. The method is used in engineering in both structural mechanics and fluid mechanics.

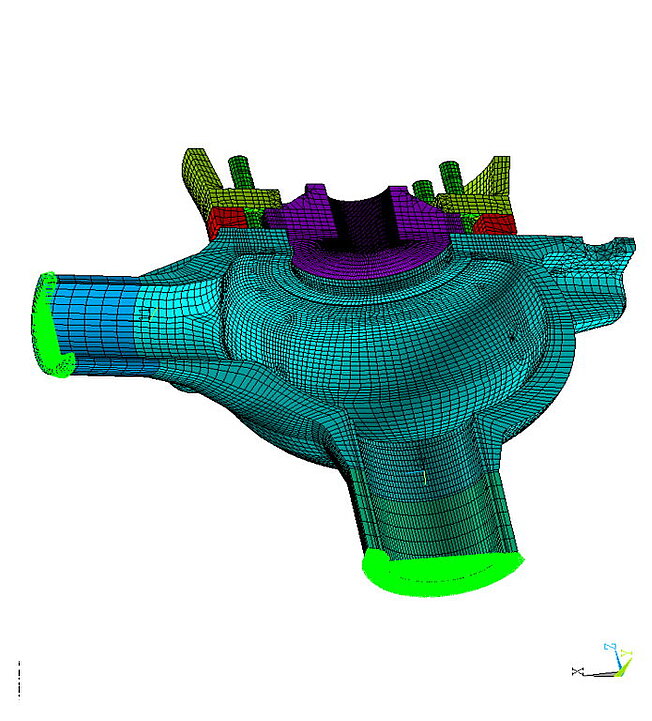
The FEM method can be used to calculate the effects of pressure, tension or torsion on bodies. Boundary conditions to a fluid such as pressure, temperature and heat transfer are only taken into account in a simplified way.

If one wants to capture the interface to fluids more precisely, a combination of FEM and CFD simulations is often used in practice.