David against Goliath or: how to build a slingshot secretly

Admittedly, the likelihood of 1. FC Heidenheim 1846 winning tomorrow night's DFB Cup quarterfinal against the great FC Bayern Munich is not all that great. As a partner & sponsor, we still reckon the FCH has a chance or two at the Allianz Arena.
Read here two possibilities, how it might work with the sensation. One of them, however, is not entirely serious.
1. we use the flow simulation
The Allianz Arena in Munich is known to resemble an oversized rubber dinghy.
Since we believe that the hardened players from the Ostalb can cope better with large masses of water than the Munich team, one possibility would be to flood the arena to keep Heidenheim's chances high. A drain on the opponent's goal would also skillfully wash the ball into the net.
Roughly calculated, the Allianz Arena has a volume of 1,330,000 m³.
One of the largest water pumps ever built by our customer KSB has a flow rate of 3.3 m³/ s.
Filling the stadium thus takes 1,330,000/3.3/3,600=111 h = 4 1/2 days.
Since FC Bayern had to play SC Freiburg away last weekend, flooding the stadium would have been possible in purely theoretical terms.
However, the disadvantage here is that the spectator area would also be flooded. In addition, no one has probably considered this special load case, so that the inflatable would burst beforehand.
2. Tee shots from the baseline directly into the opponent's goal
We probably have the better chances here, because Manuel Neuer is often very far in front of his own goal. But how fast and at what angle must the ball be kicked so that it can land in the Bayern goal?
The heart of the computational engineer beats at this possibility, because clear statements can be made here.
Without air resistance, even an eighth-grader who paid reasonably good attention in physics class could solve the problem:
When the ball is teed off at an angle of 45°, it needs an initial velocity of 113 km/h. The energy that is then in the ball is the same as that in the air.
With a ball mass of 450 g, the energy in the ball is 225 J or 0.225 kJ, or 100 g / 800 kJ *0.225 = 0.03 g roast pork.
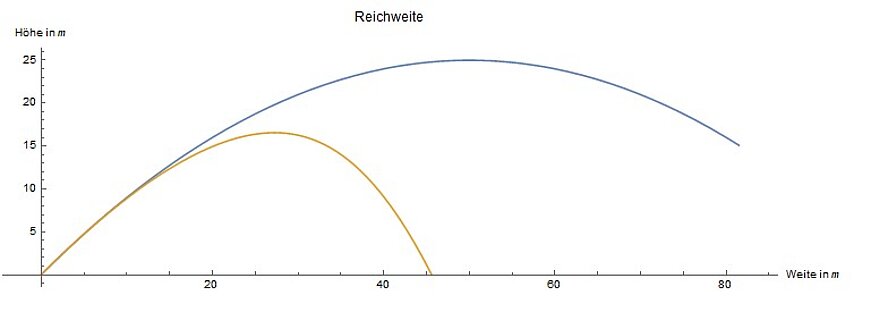
However, it becomes considerably more difficult if one wants to include the air resistance. This leads to a differential equation that makes a mathematician sweat at least slightly. After several pages of calculations, the solution looks like this:
I don't want to go into the abbreviations at all, after all I don't want to confuse you.
When you hit the ball out of the penalty area, it has to fly about 100 meters. If it were not for the air as resistance, this would also work.
However, if you compare the trajectories of the ball without (blue) and with air resistance (yellow), you will notice that the ball with resistance only falls about 45 meters.
On the Internet, you can find values of about 130-140 km/h for the maximum speeds of a soccer ball. Even if Lukas Poldolski doesn't play for FCH, our Kevin Müller can do that, too.
Let's see how far you can get with that:
With a cw value of 0.45 according to Wiki for the ball, it also stops at about 56 meters. It is also worth noting that the launch angle for the maximum distance is no longer 45°, but slightly above, at about 51°.
If the flow changes from laminar to turbulent, which is the case between 40 and 90 km/h ball speed, we have calculated with a too high drag coefficient.
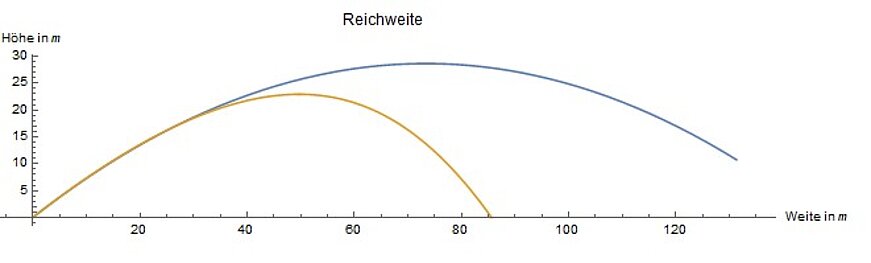
In the literature (also Wiki), cw values between 0.09 and 0.18 can be found.
This already looks better.
If we approach the subject pessimistically with the upper value of cw=0.18, this results in a distance of 85 m.
So, purely theoretically, this is possible. As a tip to Kevin Müller: hit the ball at the penalty area, angle approx. 51°, ball speed at max 140 km/h and in it goes 🙂 .
By the way, the ball is then 4.28 seconds in the air before the leather sinks behind Manuel Neuer into the net.
The trajectory with air resistance is again shown in yellow:
What you can also clearly see from the calculation examples: The cd values from the Internet are relatively wide-ranging. We can calculate them much more precisely, but that is beyond the scope of this article.
But wait, we have already calculated something...
The picture shows the flow pattern around a ball. From this, the cw value could be determined more precisely. However, we have not done this at the moment and my engineers have just made landfall.
At the time, when I asked, they said it was just to look good. That is also an argument.
So we have to rely on the rough values.
Proposal 2 now just needs to be implemented as a slingshot against Goliath, but thankfully that's not our job anymore.
Here's to a hopefully exciting game.
Your Stefan Merkle